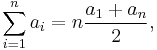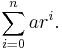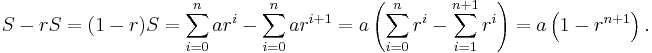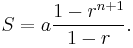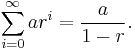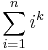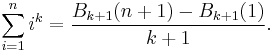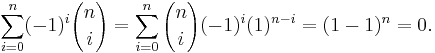Evaluating sums
In mathematics, a series is the sum of the elements of a sequence. This article mentions a few common series and how to compute their values (or prove that they do not converge). This gives more derivations than the list of mathematical series elsewhere in Wikipedia.
Contents |
Arithmetic series
The prototype of the arithmetic series is
the sum of the first n natural numbers, for any natural number n. Since it is finite, it converges, and its value can be determined using the following technique. We can rewrite the sum by "counting down" rather than "counting up"; that is, if the above series is S, then
If we now add both expressions we have
Therefore we get the fundamental identity
(This formula breaks down in some instances--- for example when performing modular arithmetic with modulus 2, this formula is nonsensical; however, in that case the sum can easily be evaluated by inspection since the terms alternate between 0 and 1).
Other arithmetic series may be computed using this calculation as a base. Given any two numbers a, d (which may be integral, real, complex, or in fact members of any abelian group at all), we may define an arithmetic progression with initial term a and difference d, whose general term is
For a fixed integer n, we can form the arithmetic series
the sum of the first n terms of this progression. If we substitute the definition of ai and use the linearity of the sum, the computation reduces to one we have just done:
This simplifies (using the definition of an) to
the average of the outer terms of the progression multiplied by the number of terms.
Geometric series
Geometric series, like arithmetic series, can be defined for any numbers (integer, real, complex, or otherwise) a and r. Due to the rules of exponentiation these series tend to be indexed from zero; a is the initial term, and r is the ratio between successive terms. Then the series is
To evaluate this series (again denoted S), a simple cancellation trick is used: if we multiply the series by r and subtract from the original, we get
Thus we get the fundamental relation
(Again, to be perfectly precise we must have r not equal to 1; in this case, the sum is easily evaluated by inspection since each power of i is also equal to 1).
If (as is usual) we are working in the real or complex numbers, and if 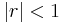 , then we can take the limit as n approaches infinity. This yields the infinite series
, then we can take the limit as n approaches infinity. This yields the infinite series
Of course, the right-hand side is valid for any number r other than 1, but only when 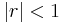 is it equal to the left-hand side. Otherwise, the series diverges (since the terms do not approach 0).
is it equal to the left-hand side. Otherwise, the series diverges (since the terms do not approach 0).
Higher powers
Other common families of series are sums of powers:
for positive integers k; the arithmetic series is the case for k equal to 1. It follows from an identity of the Bernoulli polynomials that these sums can be calculated as:
This is not as vacuous as it seems, since the Bernoulli polynomials are well-studied and their coefficients, which are related to the Bernoulli numbers, are easy to calculate.
Applications of Taylor series
Taylor series can be used to find the sum of certain series which are not obvious at first glance; by their nature, these are generally infinite series. There are several well-known examples:
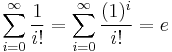 ;
;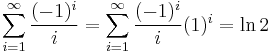
This is not immediate; the radius of convergence of the power series for 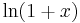 is just 1, and therefore this sum lies on the boundary. To show that the value of the power series is equal to the value of the function requires additional analysis.
is just 1, and therefore this sum lies on the boundary. To show that the value of the power series is equal to the value of the function requires additional analysis.
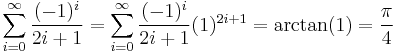 .
.
Using the binomial theorem, which is a very special case of the Taylor series (about 1) for the function 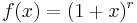 for arbitrary positive real numbers r, we can also obtain
for arbitrary positive real numbers r, we can also obtain
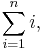
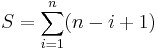
![2S = S %2B S = \sum_{i = 1}^n [i %2B (n - i %2B 1)] = \sum_{i = 1}^n (n %2B 1) = n(n %2B 1).](/2012-wikipedia_en_all_nopic_01_2012/I/dbd5f6399e06f4dd66b7590250e3c7bd.png)
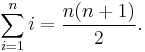
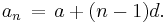
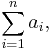
![\sum_{i = 1}^n [a %2B (i - 1)d] = n a - n d %2B d\sum_{i = 1}^n i = na - nd %2B d \frac{n(n %2B 1)}{2}.](/2012-wikipedia_en_all_nopic_01_2012/I/0dbf96a034c0b657ba5ef6be5c5e633b.png)